Genetic algorithms

Genetic Algorithms (GAs), as developed by John Holland [Hol75], are Evolutionary Algorithms that use genetic recombination as the main reproduction heuristic, accompanied with mutation.

With GAs, biological consistency is maintained to a further extent than EAs, especially when n-point crossover is used. Uniform Crossover, a given probability of cross-over at any gene, is not biologically consistent and is not widely used. There are also parallel reproductive heuristics, where multiple populations are evolved but mostly (or entirely) kept separate, Calvin [Cal04, Ch. 10] argues this has been an important extra catalyst to natural evolution. For an overview of the different reproductive heuristics read Gordon and Whitley [GW93]. All known species in nature either produce asexual (one parent) or sexual (two-parent) recombination. This restriction is not a requirement in artificial algorithms and improvements in performance have been reported when increasing the number of parents [ERR94]. Sex is another catalyst, but not an essential according to Calvin [Cal04]. Box 3.1.1 displays the pseudo-code of Holland's Simple Genetic Algorithm (SGA). [MT95]

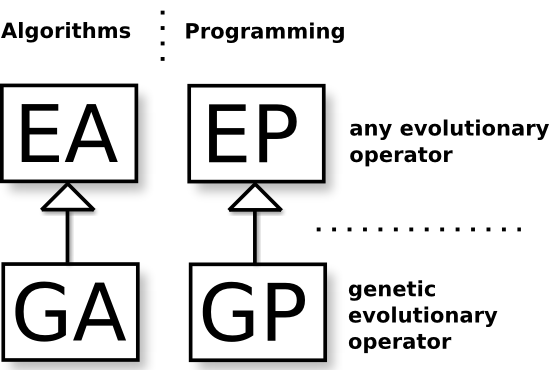
Evolutionary algorithms are also used to directly evolve lines of computer programming code, this is called Evolutionary Programming (EP) and Genetic Programming (GP) when recombination is used. The relation between these four domains is displayed in UML notation in figure 3.1.

Figure 3.1: Evoltionary Algorithms (above left), their subtype Genetic Algorithms (bottom left), Evolutionary Programming (top right) and Genetic Programming (bottom right).

In section 3.2.1 I will present an example of an application of a genetic algorithm.